Radiano

Quando tratamos de movimento circular, ao invéz de usar “graus”, usamos uma unidade de medida “radiano” (rad).
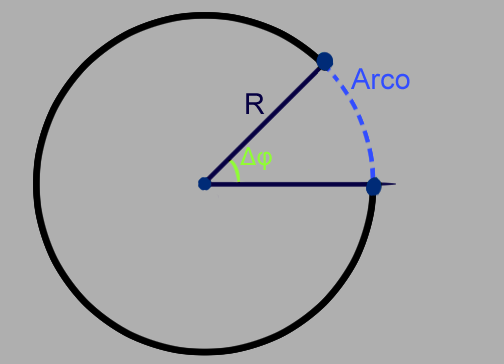
A definição do radiano é um determinado ângulo a qual tem seu arco correspondente igual ao raio da circunferência. Olhando na figura, supondo que a Δφ é igual à 1 radiano. Então o Arco destacado (que é o arco correspondente) será igual ao raio R.
O valor do radiano é determinado da seguite maneira:
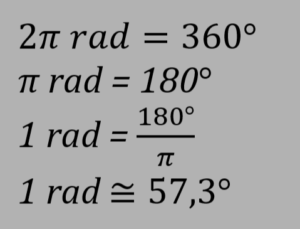
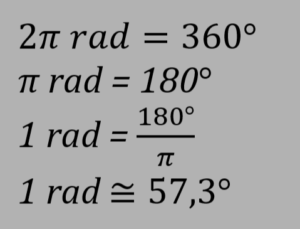
Para converter o radiano em graus, basta multiplicar o valor pela 180/π. Exemplos:
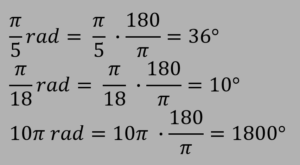
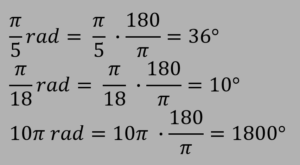
E quantas voltas é representado pelo 4π rad? Duas voltas. Porque se 2π rad é uma volta, 4π rad (o dobro) será duas voltas. E 5π rad? Duas voltas e meia.
Periodo
Período (T) é o tempo que o corpo em movimento circular leva para completar uma volta completa.
Por exemplo, se um objeto leva 5 segundos para completar 1 volta, o período seria 5 segundos. Se um objeto fez 5 voltas em 1 segundo, o período seria 1/5 = 0,20 segundos.
Então a formula geral é:
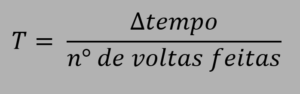
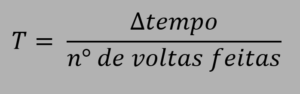
Frequência
Frequência (f) é o número de voltas que um corpo completa em um determinado intervalo de tempo. É contada em Hertz (hz) (rotações por segundo), rpm (rotações por minuto) ou até rph (rotações por hora). É o inverso do período.
Se um objeto leva 5 segundos para completar 1 volta, a frequência seria 1/5 voltas por segundo, ou 0,20 Hz. Se um objeto fez 5 voltas em 1 segundo, a frequência seria 5/1 = 5 Hz.
Então a formula geral é:
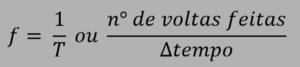
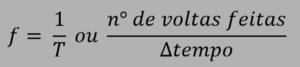
Praticando
Um corpo realiza uma volta completa da sua trajetória em 10 ms (milisegundo). Defina sua frequência em Hertz e periodo de rotação em segundos. (1 s = 1000 ms)
Primeiro, vamos realizar as converções de unidades para facilitar o calculo. Já que o exercício está pedindo em segundos, converteremos ms para s. (conceito tratado no artígo “grandezas físicas”)
Como dado no enunciado, 1 s = 1000ms. Agora basta realizar uma simples regra de três.
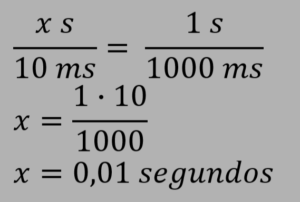
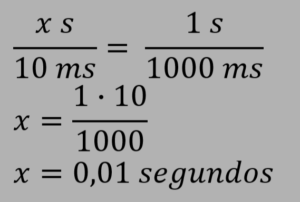
Ou seja, o corpo realiza uma volta completa em 0,01 s (10 ms). Este seria o periodo da rotação.
A frequência será, então:


Resumo


