

Lançamento Oblíquo
Lançamento oblíquo. Nessa imagem, a atleta joga a lança e a lança irá descrever uma parábola, como illustrada na figura abaixo. Tratamos de um lançamento oblíquo.
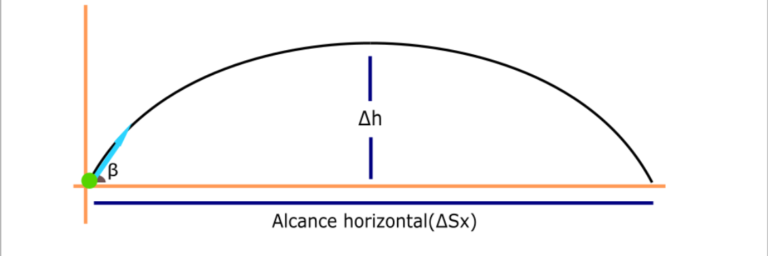

Para analisar o lançamento oblíquo, também devemos olhar para o movimento em duas dimensões – dimensão dos vetores verticais e dimensão dos vetores horizontais. Mas perceba que diferente de lançamentos horizontais, lançamentos oblíquos envolvem uma subida e uma descida, desenvolvendo assim, uma parabola.
Sobre a influência da gravidade, o vetor vertical parte com valor positivo (ou seja, sobe a parabola) e acaba com valor negativo (acelerando para a terra), enquanto o vetor de velocidade horizontal se mantém (igual ao caso do lançamento horizontal). Temos:
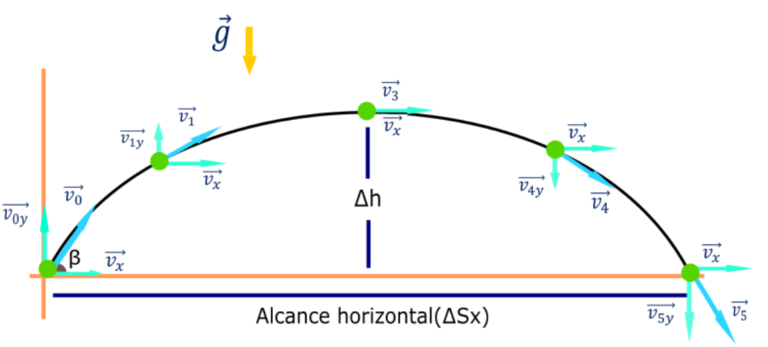

Vamos começar nosso análise com o vetor velocidade inicial. Observe:
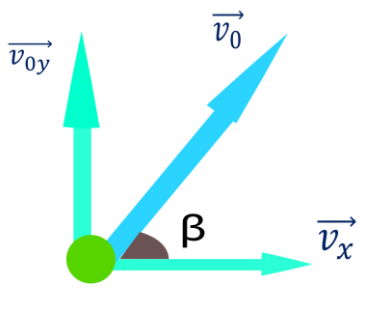

Após a decomposição do V0, temos vetores Voy (Velocidade inicial na dimensção vertical) e Vx (vetor velocidade na dimensão horizontal ). Obteremos o valor deles usando conceito de seno e cosseno.
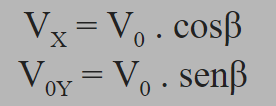
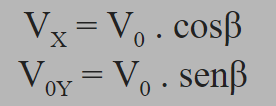
Agora, prosseguimos a análise dividindo o movimento em duas dimensões, que nem no lançamento horizontal.
Já que o vetor velocidade da lança é sempre inclinada em relação à terra, é possível decompr o movimento em um vetor velocidade que é paralelo ao chão (dimensão horizontal) e vetor velocidade que é perpendicular ao chão (dimensão vertical). Analisando o movimento em dimensões seperadas (em outras palavras, analisando as duas composnentes do movimento) nos ajuda a compreender melhor o movimento inteiro.
Dimensão Horizontal
Quando a lança sai da mão da atleta, não há nada no ar que lhe acelera. A lança mantém a velocidade .
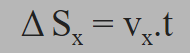
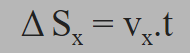
A Delta Sx é a variação horizontal, Vx sendo a velocidade horizontal e t, tempo de voo.
Dimensão Vertical
A seguir, vamos analisar a dimensão vertical.
Começamos por tentar descubrir o tempo de subida da lança. Aqui na dimensão horizontal tratamos de um Movimento Uniformemente Variado (devido à presença da gravidade), podemos usar a fórmula de “vovô ateu”, onde a aceleração será a gravidade; Vy, a velocidade final na subida; Voy, a velocidade inicial; e t, tempo de subida.
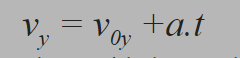
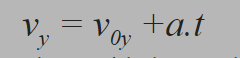
Primeiro, vale reconhecer que a aceleração da gravidade tem direção oposta do referencial, podemos então, atribuir o sinal negativo para ele.
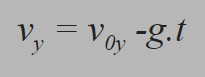
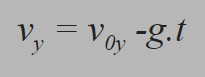
Segundo, quando a bola atinge a altura máxima, o Vy (velocidade vertical) será nula (0 m/s), porque se trata de um instante na qual a direção vertical da bola muda de sentido (de cima para baixo / de positivo para negativo). Portanto:
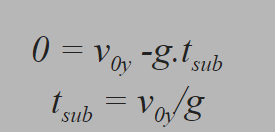
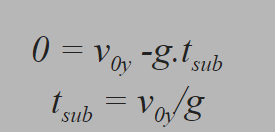
E assim, obtemos o tempo de subida. A qual é uma função de velocidade verticla inicial e a aceleração da gravidade.
Agora pare e olhe para a ilustração: é fácil perceber que a trajetória da bola é simétrica. Ou seja, o tempo de subida para a altura máxima (onde que se encontra V3 na figura) é igual ao resto do tempo de voo da bola (ou, a tempo de queda). Isso quer dizer que o tempo total de voo [e o dobro do tempo de subida. Portanto:
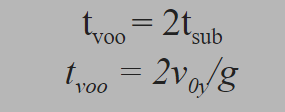
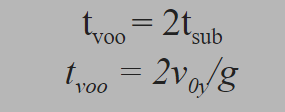
Partimos para descubrir a altura máxima atingida pela lança. Usaremos a equação da Torricelli. Tendo em mente que velocidade vertical na altura máxima é nula, temos:
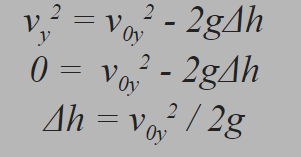
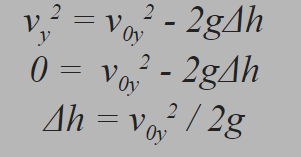
Praticando
Uma pessoa chuta uma bola. A bola desenvolve uma velocidade de 10m/s e em um ângulo de 20 graus em relação ao chão.
Desprezando a resistência do ar…
Dado: SEN 20 = 0,34/ COS 20 = 0,94/ aceleração da gravidade = 10m/s^2
Qual velocidade horizontal e vertical da bola no instante t = 0s?
Lembra de descubrir os vetores velocidades por meio de seno e cosseno? Use isso.
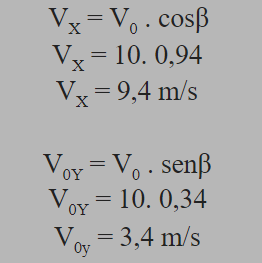
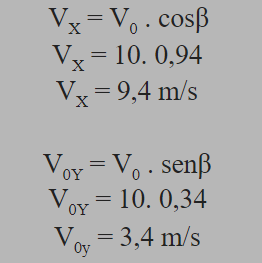
A bola termina o percurso em quanto tempo?
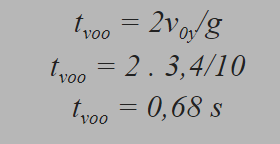
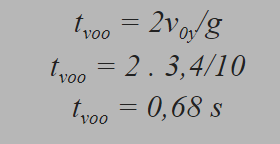
Qual o alcance horizontal da bola?
Tendo o tempo de voo, basta só usar a fórmula do MRU:
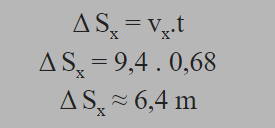
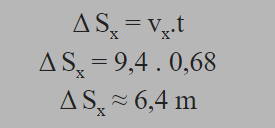
Qual a altura máxima atingida pela bola?
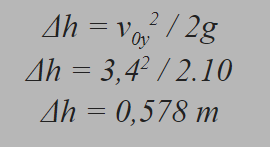
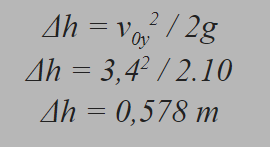
Resumo


