Observe a figura abaixo:
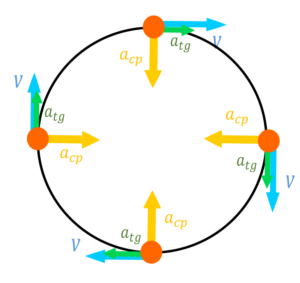

O vetor velocidade é sempre TANGENCIAL à trajetória circular, portanto o vetor aceleração dessa também é tangencial à trajetória circular. Agora perceba que a velocidade, justamente porque se mantém tangente à trajetória circular, muda de direção constantemente. Para que isso aconteça, é necessária uma aceleração centrípeta (que aponta para o centro).
Aceleração tangencial
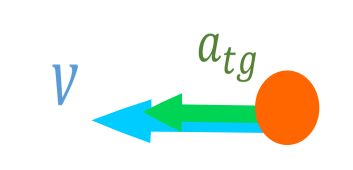

A aceleração tangencial é a mesma aceleração que estudamos no Movimento Retilíneo Uniformemente Variado. Quando uma aceleração possui a mesma direção da velocidade, ela é chamada de aceleração tangencial (tangente à trajetoria). Ou seja, é igual à aceleração linear ou escalar do MUV. Portanto podemos aplicar as equações do MUV para calculá-lo. (como o Sorvetão e Torricelli).
Quando a aceleração tangencial é positiva, o giro do objeto em movimento torna mais rápido; quando a aceleração tangencial é negativa, o giro torna mais lenta até parar; quando a aceleração tangencial é nula, o objeto desenvolve giros com velocidade uniforme.


Aceleração centripeta
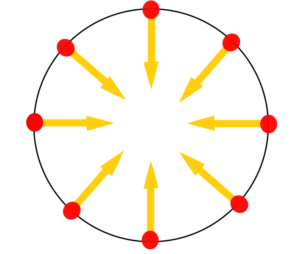

Todo movimento curvilíneo tem uma aceleração centrípeta.
A aceleração centripeta, como o nome mesmo indica, é o responsável pela mudança de direção do objeto em movimento. Perceba que em um movimento circular/curvilíneo, o vetor velocidade muda constantemente de direção e sentido. Essa constante mudança é a aceleração centripeta em ação.
A alteração na aceleração centrípeta depende da velocidade tangencial desenvolvida pelo objeto e o raio da trajetória desenvolvida.


Aceleração vetorial
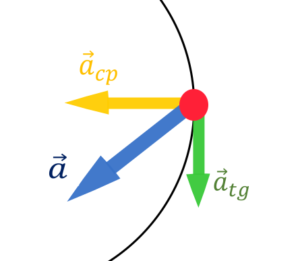

A aceleração vetorial é simplesmente a soma das aceelrações centrípetas e tangenciais.
Como o próprio nome já diz, a aceleração tangencial é tangente à trajetória e consequentemente perpendicular à aceleração centrípeta (que aponta para o centro da trajetória curvilínea). Portanto para calcular a resultante (soma) entre as duas acelerações, podemos usar a teorema de pitágoras e lei do seno cosseno e tangente.
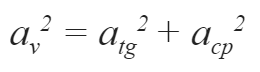
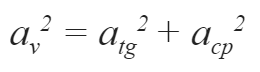
Aceleração vetorial
Em uma virada, uma trem realiza uma trajetória curvilínea com raio de 100 metros. No instante t = 0, o trem desenvolve uma velocidade de 18km/h e está desacelerando o trem 1m/s cada segundo. Pergunta-se:
1. Qual a aceleração centrípeta desenvolvida pela trem no momento t = 1,5 s?
Para calcular a velocidade centrípeta, é necessária saber o raio (nesse caso seria 100 metros) e a velocidade desenvolvida por ela no instante. Primeiro, já que a unidade de medida do dado oferecido pelo enunciado é em km/h, é melhor fazer primeiro a conversão para m/s a fim de facilitar o calculo.
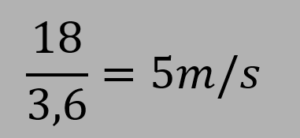
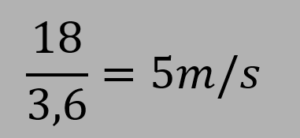
Agora, sabendo que o veículo está alterando (desacelerando), precisamos calcular agora a velocidade do trem no tempo pedido (1,5s).
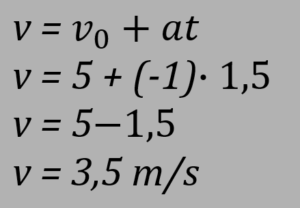
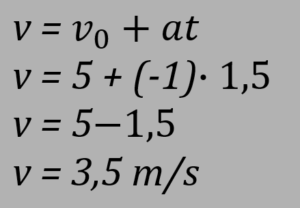
Tendo a velocidade e o raio da trajetória, calculamos a aceleração centrípeta:
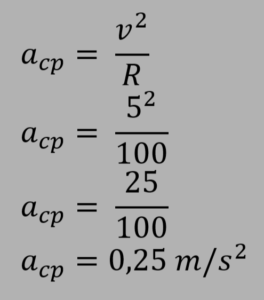
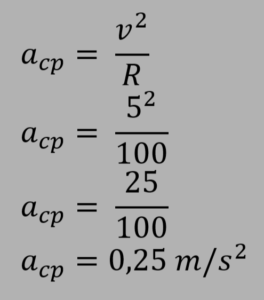
2. Qual o módulo da aceleração vetorial (aceleração resultante) nos intante t = 1,5 s ?
Primeiro vamos illustrar a problema:
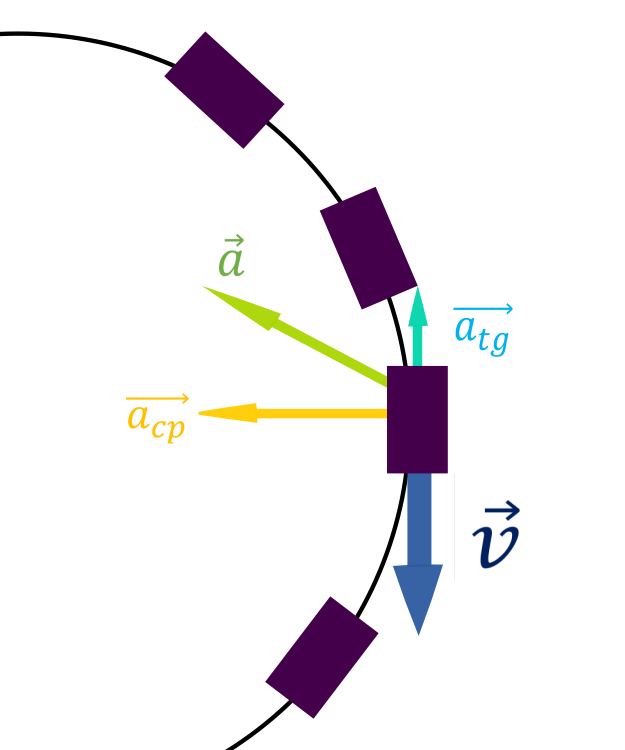

Como sabemos, a aceleração vetorial é a soma da aceleração centrípeta e tangencial. Usaremos teorema de pitágoras.
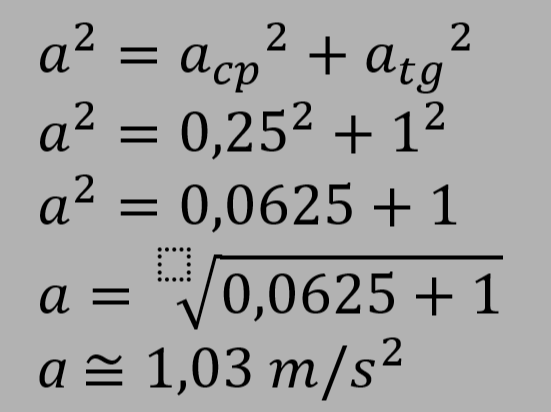
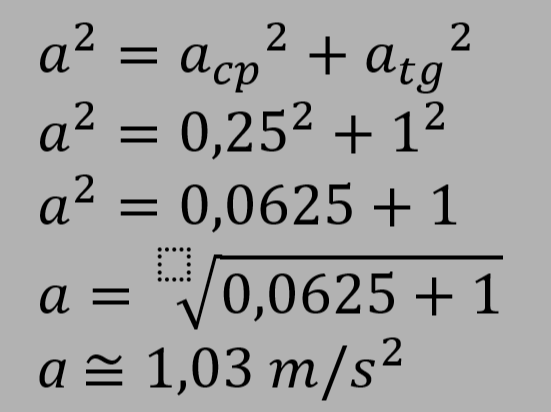
Resumo


